Prerequisites: Clustering in machine learning
What is Clustering?
Clustering is an unsupervised machine learning technique that divides a given piece of data into different clusters based on its distance (similarity) from each other.
The unsupervised k-means clustering algorithm sets the value of any point in a particular cluster to 0 or 1, i.e., true or false. However, fuzzy logic gives fuzzy values for any particular data point located in either group set. Here, in fuzzy C-means clustering, we find the centroid of the data points and then calculate the distance of each data point from the given centroid until the resulting cluster becomes constant.
Suppose the given data points are {(1, 3), (2, 5), (6, 8), (7, 9)}
The steps to execute the algorithm are:
Step 1: Initialize the data points randomly to the desired number of clusters.
Suppose you have two clusters in which you want to divide the data, initialize the data points randomly. Each data point is in two clusters, and they have some membership value, any of which can be assumed in the initial state.
The following table represents the values of the data points in each cluster and their membership (gamma).
Cluster (1, 3) (2, 5) (4, 8) (7, 9)
1) 0.8 0.7 0.2 0.1
2) 0.2 0.3 0.8 0.9Step 2: Find out the centroid.
The formula for finding the centroid (V) is:
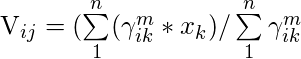
Among them, μ is the fuzzy membership value of the data point, m is the fuzzy parameter (generally 2), and xk is the data point.
Over here
V11 = (0.82 *1 + 0.72 * 2 + 0.22 * 4 + 0.12 * 7) /( (0.82 + 0.72 + 0.22 + 0.12 ) = 1.568
V12 = (0.82 *3 + 0.72 * 5 + 0.22 * 8 + 0.12 * 9) /( (0.82 + 0.72 + 0.22 + 0.12 ) = 4.051
V11 = (0.22 *1 + 0.32 * 2 + 0.82 * 4 + 0.92 * 7) /( (0.22 + 0.32 + 0.82 + 0.92 ) = 5.35
V11 = (0.22 *3 + 0.32 * 5 + 0.82 * 8 + 0.92 * 9) /( (0.22 + 0.32 + 0.82 + 0.92 ) = 8.215
Centroids are: (1.568, 4.051) and (5.35, 8.215)Step 3: Find out the distance from each point to the centroid.
D11 = ((1 - 1.568)^2 + (3 - 4.051)^2)^0.5 = 1.2
D12 = ((1 - 5.35)^2 + (3 - 8.215)^2)^0.5 = 6.79Similarly, the distances of all other points are calculated from the two centroids.
Step 4: Update the membership value.
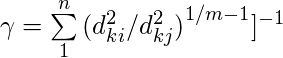
The new member values for point 1 are:
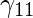
\gamma_{11} = [{ [(1.2)^2 / (1.2)^2] + [(1.2)^2 / (6.79)^2]} ^ {(1 / (2 – 1))} ]^-1 = 0.96
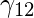
\gamma_{12} = [{ [(6.79)^2 / (6.79)^2] + [(6.79)^2 / (1.2)^2]} ^ {(1 / (2 – 1))} ]^-1 = 0.04
or
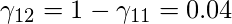
Again, all other membership values are calculated, and the matrix is updated.
Step 5: Repeat steps (2-4) until the constant value or difference of the obtained membership value is less than the tolerance value (a smaller value that allows the difference of two subsequent updated values to be accepted).
Step 6:
Obfuscation of the obtained membership value.
Implementation: The Fuzzy scikit learning library has predefined functions for Fuzzy C means that can be used in Python. To use fuzzy C-means, you need to install the skfuzzy library.
pip install sklearn
pip install skfuzzy