Additional tips for SEO:
In machine learning and data science, we often encounter a problem called data distribution imbalance, which usually occurs when one class has much higher or lower observations than the others. Since machine learning algorithms tend to improve accuracy by reducing errors, they don’t take into account the distribution of classes. This problem is prevalent in the following examples: fraud recognition, anomaly detection, facial recognition, and so on
Standard ML techniques such as decision trees and logistic regression tend to ignore minorities for the majority class. They only tend to predict majorities, and as a result, the classification of minorities is significantly wrong compared to majorities. To put it more technically, if the distribution of data in our dataset is unbalanced, then our model is more prone to cases where minority categories are negligible or less recalled.
Unbalanced data processing techniques: There are two main algorithms, which are widely used to deal with unbalanced class distributions.
- SMOTE
- Near Miss algorithm
SMOTE (Integrated Sampling Technology for Ethnic Minorities) – Oversampling
SMOTE (Synthetic Minority Oversampling Technique) is one of the most commonly used oversampling methods to address imbalances.
Its purpose is to balance the class distribution by randomly copying examples of minorities.
SMOTE synthesizes new minority instances between existing minority instances. It produces
Virtual training records for linear interpolation
Minorities. These comprehensive training records are generated by randomly selecting one or more k-nearest neighbors for each example in the minority category. After oversampling, the data is reconstructed, and several classification models can be applied to the processed data.
More insights on how the SMOTE algorithm works!
Step 1:
Set up minorities
A
each
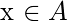
,
k neighbors of x
Calculated by
Euclidean distance
between
X
and all other samples in the collection
A
.
Step 2:
Sample rate
ñ
Set according to the proportion of imbalance. For each
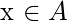
,
ñ
instances (i.e. x1, x2, …) xn) is randomly selected from its k nearest neighbors, and they make up the set
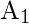
.
Step 3:
For each example

(k = 1, 2, 3… N), the following formula is used to generate a new example:
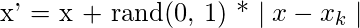
where rand(0, 1) represents a random number between 0 and 1.
NearMiss Algorithm – Undersampling
NearMiss is an undersampling technique. It is designed to balance class assignments by randomly eliminating majority class examples. When two instances of different classes are very close to each other, we remove the instances of the majority class to increase the space between the two classes. This helps in the classification process.
To prevent problems
Loss of information
In most undersampling techniques,
Neighbor
Methods are widely used.
The basic intuitions about the work of the nearest neighbor method are as follows:
Step 1: The method first finds the distance between all instances of the majority class and the instances of the minority class. Here, most categories will be undersampled.
Step 2: Then, select n instances of the majority class that have the smallest distance from the instances in the minority class.
Step 3: If there are k instances in the minority class, the closest method will arrive at k * n instances in the majority class.
In order to find n closest instances in most classes, there are several variations of the NearMiss algorithm:
- NearMiss – Version 1: It selects a sample of the majority class with the smallest instance of the minority group with an average distance of k.
- NearMiss – Version 2: It selects a sample of the majority class with the smallest instances of the minority group with an average distance of k.
- NearMiss – Version 3: It works in two steps. First, for each minority instance, M nearest neighbors will be stored. Then, finally, select the majority of class instances, which have the greatest average distance from the N nearest neighbors.
This article provides a better understanding and hands-on practice on how to best choose between different unbalanced data processing techniques.
Load libraries and data files
The dataset consists of transactions made by credit cards. The dataset has:
492 fraudulent transactions out of 284,807 transactions
。 This makes it highly unbalanced, with the positive category (fraud) accounting for 0.172% of all transactions.
Datasets can be downloaded from the following locations
Over here
.
# import necessary modules
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix, classification_report
# load the data set
data = pd.read_csv( 'creditcard.csv' )
# print info about columns in the dataframe
print (data.info())The output is as follows:
RangeIndex: 284807 entries, 0 to 284806
Data columns (total 31 columns):
Time 284807 non-null float64
V1 284807 non-null float64
V2 284807 non-null float64
V3 284807 non-null float64
V4 284807 non-null float64
V5 284807 non-null float64
V6 284807 non-null float64
V7 284807 non-null float64
V8 284807 non-null float64
V9 284807 non-null float64
V10 284807 non-null float64
V11 284807 non-null float64
V12 284807 non-null float64
V13 284807 non-null float64
V14 284807 non-null float64
V15 284807 non-null float64
V16 284807 non-null float64
V17 284807 non-null float64
V18 284807 non-null float64
V19 284807 non-null float64
V20 284807 non-null float64
V21 284807 non-null float64
V22 284807 non-null float64
V23 284807 non-null float64
V24 284807 non-null float64
V25 284807 non-null float64
V26 284807 non-null float64
V27 284807 non-null float64
V28 284807 non-null float64
Amount 284807 non-null float64
Class 284807 non-null int64# normalise the amount column
data[ 'normAmount' ] = StandardScaler().fit_transform(np.array(data[ 'Amount' ]).reshape( - 1 , 1 ))
# drop Time and Amount columns as they are not relevant for prediction purpose
data = data.drop([ 'Time' , 'Amount' ], axis = 1 )
# as you can see there are 492 fraud transactions.
data[ 'Class' ].value_counts()The output is as follows:
0 284315
1 492Divide the data into a test set and a training set
from sklearn.model_selection import train_test_split
# split into 70:30 ration
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3 , random_state = 0 )
# describes info about train and test set
print ( "Number transactions X_train dataset: " , X_train.shape)
print ( "Number transactions y_train dataset: " , y_train.shape)
print ( "Number transactions X_test dataset: " , X_test.shape)
print ( "Number transactions y_test dataset: " , y_test.shape)The output is as follows:
Number transactions X_train dataset: (199364, 29)
Number transactions y_train dataset: (199364, 1)
Number transactions X_test dataset: (85443, 29)
Number transactions y_test dataset: (85443, 1)Now train the model without dealing with an unbalanced class distribution
# logistic regression object
lr = LogisticRegression()
# train the model on train set
lr.fit(X_train, y_train.ravel())
predictions = lr.predict(X_test)
# print classification report
print (classification_report(y_test, predictions))The output is as follows:
precision recall f1-score support
0 1.00 1.00 1.00 85296
1 0.88 0.62 0.73 147
accuracy 1.00 85443
macro avg 0.94 0.81 0.86 85443
weighted avg 1.00 1.00 1.00 85443The accuracy is 100%, but have you noticed something strange?
There are very few recalls from the minority class. It turns out that the model is more majoritarian. Therefore, it turns out that this is not the best model.
Now, we’ll apply a different one
Unbalanced data processing techniques
and see its accuracy and recall results.
The SMOTE algorithm is used
You can check all the parameters from here.
print ( "Before OverSampling, counts of label '1': {}" . format ( sum (y_train = = 1 )))
print ( "Before OverSampling, counts of label '0': {} \n" . format ( sum (y_train = = 0 )))
# import SMOTE module from imblearn library
# pip install imblearn (if you don't have imblearn in your system)
from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state = 2 )
X_train_res, y_train_res = sm.fit_sample(X_train, y_train.ravel())
print ( 'After OverSampling, the shape of train_X: {}' . format (X_train_res.shape))
print ( 'After OverSampling, the shape of train_y: {} \n' . format (y_train_res.shape))
print ( "After OverSampling, counts of label '1': {}" . format ( sum (y_train_res = = 1 )))
print ( "After OverSampling, counts of label '0': {}" . format ( sum (y_train_res = = 0 )))The output is as follows:
Before OverSampling, counts of label '1': [345]
Before OverSampling, counts of label '0': [199019]
After OverSampling, the shape of train_X: (398038, 29)
After OverSampling, the shape of train_y: (398038, )
After OverSampling, counts of label '1': 199019
After OverSampling, counts of label '0': 199019See!
The SMOTE algorithm oversamples a small number of instances so that they are equal to the majority class. The number of records is equal for both categories. More specifically, minorities have increased to the total number of majorities.
Now, after applying the SMOTE algorithm (oversampling), the accuracy and recall results can be seen.
Prediction and recall
lr1 = LogisticRegression()
lr1.fit(X_train_res, y_train_res.ravel())
predictions = lr1.predict(X_test)
# print classification report
print (classification_report(y_test, predictions))The output is as follows:
precision recall f1-score support
0 1.00 0.98 0.99 85296
1 0.06 0.92 0.11 147
accuracy 0.98 85443
macro avg 0.53 0.95 0.55 85443
weighted avg 1.00 0.98 0.99 85443wow
Compared to the previous model, our accuracy was reduced to 98%, but the recall value for minorities was also improved by 92%. This is a good model compared to the previous one. It’s great in retrospect.
Now, we will apply the NearMiss technique to undersample most of the categories to see their accuracy and recall results.
NearMiss Algorithm:
You can check all the parameters from here.
print ( "Before Undersampling, counts of label '1': {}" . format ( sum (y_train = = 1 )))
print ( "Before Undersampling, counts of label '0': {} \n" . format ( sum (y_train = = 0 )))
# apply near miss
from imblearn.under_sampling import NearMiss
nr = NearMiss()
X_train_miss, y_train_miss = nr.fit_sample(X_train, y_train.ravel())
print ( 'After Undersampling, the shape of train_X: {}' . format (X_train_miss.shape))
print ( 'After Undersampling, the shape of train_y: {} \n' . format (y_train_miss.shape))
print ( "After Undersampling, counts of label '1': {}" . format ( sum (y_train_miss = = 1 )))
print ( "After Undersampling, counts of label '0': {}" . format ( sum (y_train_miss = = 0 )))The output is as follows:
Before Undersampling, counts of label '1': [345]
Before Undersampling, counts of label '0': [199019]
After Undersampling, the shape of train_X: (690, 29)
After Undersampling, the shape of train_y: (690, )
After Undersampling, counts of label '1': 345
After Undersampling, counts of label '0': 345The NearMiss algorithm undersamples most of the instances so that they are equal to the majority of classes. Here, the majority class has been reduced to the total number of minority classes, so the number of records is equal for both classes.
Prediction and recall
# train the model on train set
lr2 = LogisticRegression()
lr2.fit(X_train_miss, y_train_miss.ravel())
predictions = lr2.predict(X_test)
# print classification report
print (classification_report(y_test, predictions))The output is as follows:
precision recall f1-score support
0 1.00 0.56 0.72 85296
1 0.00 0.95 0.01 147
accuracy 0.56 85443
macro avg 0.50 0.75 0.36 85443
weighted avg 1.00 0.56 0.72 85443This model is better than the first one because it classifies better and has a recall value of 95% for a few categories. However, due to insufficient sampling of the majority stratum, the recall rate has dropped to 56%. So, in this case, SMOTE provided me with a high accuracy and recall, and I will continue to use the model! 🙂
First, your interview preparation enhances your data structure concepts with the Python DS course.