Hill climbing is a heuristic search that is used for mathematical optimization problems in the field of artificial intelligence.
Given a lot of input and good heuristics, it will try to find a good enough solution to the problem. The solution may not be the global optimal maximum.
- In the above definition, mathematically optimized problems mean that climbing a mountain solves the problem where we need to maximize or minimize a given real function by selecting values from a given input. Example-Traveling Salesman Problem: We need to minimize the distance a salesman travels.
- “Heuristic search” means that the search algorithm may not find the best solution to the problem. However, it will provide a good solution at a reasonable time.
- A heuristic is a feature that ranks all possible alternatives in any branching step of the search algorithm based on the available information. It helps the algorithm to choose the best route from the possible routes.
Features of mountain climbing
1. Variants of Build and Test Algorithms: It is a variant of building and testing algorithms. The algorithm for building and testing is as follows:
1. Generate possible solutions.
2. Test to see if this is the expected solution.
3. If you find a solution, quit, otherwise go to step 1.
Therefore, we refer to Hill Climb as a variant of the build and test algorithm because it takes feedback from the testing process. The builder will then use this feedback to determine the next action in the search space.
2. Use a greedy approach: At any point in the state space, the search only moves in that direction, which optimizes the cost of functionality and hopefully finds the best solution in the end.
Types of climbs
Simple hill climb: It examines neighboring nodes one by one and then selects the first neighbor node that optimizes the current cost as the next node.
Simple Hill Climbing Algorithm:
Step 1: Evaluate the initial status. If it is the target state, it stops and returns success. Otherwise, the initial state is set to the current state.
Step 2: Loop until a solution state is found, or no new operator exists that can be applied to the current state.
a) Select a state that has not yet been applied to the current state and apply it to produce a new state.
b) Perform these actions to evaluate the new status
i. If the current state is the target state, it stops and returns success.
ii。 If it’s better than the current state, make it the current state and proceed.
iii。 If it’s not better than the current state, then keep the cycle until a solution is found. Step 3: Exit.
Steepest hill climb: It first checks all adjacent nodes, and then selects the node closest to the solution state from the next node.
Step 1: Evaluate the initial status. If it is the target state, exit it, otherwise set the current state to the initial state. Step 2: Repeat these steps until a solution is found or the current state remains the same. Suppose the “target” is a state so that any successor to the current state is better than it. ii。 For each operator that applies to the current state, a new operator is applied and a new state b is created. Assess the new status c. If this status is a target state, it exits, otherwise it is compared to Target. If this status is better than Target, then set this status to Target e. If the target is better than the current state, then set the current state to the target Step 3: Exit
Random hill climbing:
It doesn’t check all neighboring nodes until it decides which node to choose. It simply randomly selects a neighbor and decides (based on the amount of improvement on that neighbor) whether to move to that neighbor or check another.
Spatial diagram of the hill climbing state
A state-space graph is a graphical representation of the value of the set of states that our search algorithm can achieve versus the objective function (the function we wish to maximize).
X-axis: represents the state space, i.e. the state or configuration that our algorithm may reach.
Y-axis: Represents the value of the objective function corresponding to a specific state.
The best solution is for the objective function to have a state space with a maximum value (global maximum).
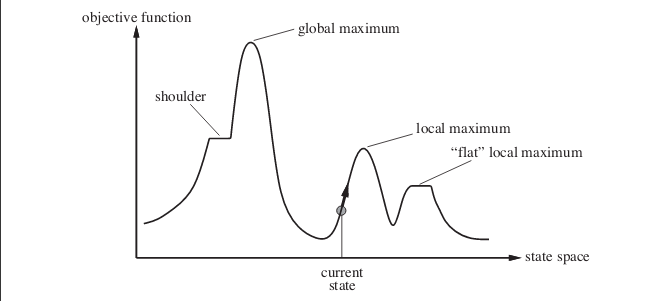
Different areas in a state-space diagram
- Local maximum: It is a better state than its neighbors, but there is a better state than its neighbors (global maximum). This state is better because here the value of the objective function is higher than the value of its neighbor function.
- Global maximum: This is the best state in the state space diagram. This is because in this state, the objective function has the highest value.
- Plateau/Flat Local Max: It is a flat region of the state space where adjacent states have the same value.
- Ridge: It is an area that is higher than its neighbors but has its own slope. This is a special type of local maximum.
- Current State: The area of the state-space diagram where we are currently during the search.
- Shoulder width: This is an uphill plateau.
Problems in different areas of mountaineering
If you climb into any of the following areas, you will not be able to reach the best/best (global maximum):
Local maximum: At the local maximum, the values of all adjacent states are worse than the current state. Since mountain climbing uses greedy methods, the mountain climb does not move to a worse state and terminates on its own. Even if a better solution may exist, the process will come to an end.
To overcome the biggest local problem: use backtracking techniques. Maintain a list of access statuses. If the search reaches a bad state, you can go back to the previous configuration and explore the new path.
Plateau: On the plateau, all neighbors have the same value. Therefore, it is not possible to choose the best direction.
Overcoming the Plateau: The Great Leap Forward. Randomly select a state that is far from the current state. We will most likely land on ridges in non-plateau areas
Any point on the ridge may look like a peak, as the movement in all possible directions is downward. As a result, the algorithm stops when it reaches this state.
Overcoming Ridge:
In this handicap, use two or more rules before testing. It means moving in multiple directions at once.