Prerequisites: K-means clustering
Spectral clustering is an evolving clustering algorithm that outperforms many traditional clustering algorithms in many cases. It treats each data point as a graph node, thus transforming the clustering problem into a graph partitioning problem. A typical implementation consists of three basic steps:
To build a similarity map:
This step constructs a similarity map in the form of an adjacency matrix represented by A. Adjacency matrices can be constructed as follows:-
- Epsilon Neighborhood Map: Pre-fixed parameter ε. Each point will then be connected to all points in its epsilon radius. If the proportions of all distances between any two points are similar, the weights of the edges, i.e., the distance between the two points, are usually not stored, because they do not provide any other information. Therefore, in this case, the constructed graph is undirected and unweighted.
- The nearest neighbor parameter k is prefixed. Then, for the two vertices of you and v, the edge is pointed from u to v only if v is in k neighbors of u. Note that this results in the formation of a weighted directed graph, as this is not always the case, for every u with v as one of k neighbors, the case will be the same for k neighbors with v neighbors. To make the graph undirected, use one of the following methods:
- If either v is in the k neighbors of u, then directing the edge of u from u to v, and directing from v to uORu is one of v’s k neighbors.
- If v is in k neighbors of u, then the edge is directed from u to v, and from v to u and u is one of v’s k neighbors.
- Fully Connected Graph: To construct this graph, each point is connected with an undirected edge weight, which is weighted by the distance between the two points and the other points. Since this method is used to model local neighborhood relationships, the Gaussian similarity measure is often used to calculate distances.
Project data into a lower dimension space:
This step is performed to account for the possibility that members of the same cluster may be very far apart in a given dimensional space. Therefore, the dimension space is reduced, so that the points are closer together in the dimensionality reduction space, so they can be clustered together by traditional clustering algorithms. By calculation
Tulapras matrix
。 First of all, the calculations need to be made, and the degree of nodes needs to be defined. The degree of the ith node is
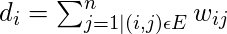
note

is the edge between nodes i and j defined in the adjacency matrix above.
The degree matrix is defined as follows:

Therefore, the Tulapras matrix is defined as:

This matrix is then normalized to improve mathematical efficiency. In order to reduce the size, firstly, the eigenvalues and the corresponding eigenvectors are calculated. If the number of clusters is k, the first eigenvalues and their eigenvectors are taken and stacked into the matrix, so that the eigenvectors become columns.
Cluster data:
This process primarily involves clustering simplified data by using any of the traditional clustering techniques, typically K-Means clustering. First, assign a row of Graph Laplace matrices to each node. Then, cluster that data using any of the traditional techniques. In order to transform the clustering results, the node identifier is preserved.
Characteristic:
- Fewer assumptions: Unlike other traditional techniques, this clustering technique does not assume that the data follows certain attributes. Thus, this enables the technique to answer more general clustering questions.
- Easy to implement and speed: The algorithm is easier to implement than other clustering algorithms and is also very fast because it consists mostly of mathematical calculations.
- Non-scalable: Because it involves the construction of matrices and the calculation of eigenvalues and eigenvectors, it is time-consuming for dense datasets.
The following steps demonstrate how to implement spectral clustering using Sklearn. The following steps of the data are credit card information that can be downloaded from Kagler.
Step 1: Import the libraries you want
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import SpectralClustering
from sklearn.preprocessing import StandardScaler, normalize
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_scoreStep 2: Load and clean the data
# Changing the working location to the location of the data
cd "C:\Users\Dev\Desktop\Kaggle\Credit_Card"
# Loading the data
X = pd.read_csv( 'CC_GENERAL.csv' )
# Dropping the CUST_ID column from the data
X = X.drop( 'CUST_ID' , axis = 1 )
# Handling the missing values if any
X.fillna(method = 'ffill' , inplace = True )
X.head()
Step 3: Preprocess the data to make the data visualized
# Preprocessing the data to make it visualizable
# Scaling the Data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Normalizing the Data
X_normalized = normalize(X_scaled)
# Converting the numpy array into a pandas DataFrame
X_normalized = pd.DataFrame(X_normalized)
# Reducing the dimensions of the data
pca = PCA(n_components = 2 )
X_principal = pca.fit_transform(X_normalized)
X_principal = pd.DataFrame(X_principal)
X_principal.columns = [ 'P1' , 'P2' ]
X_principal.head()
Step 4: Build a clustering model and visualize clustering
In the following steps, two spectral clustering models with different values will be used for the parameter Affinity. You can read the documentation about the “Spectral Clustering” class here.
a) affinity=”rbf”
# Building the clustering model
spectral_model_rbf = SpectralClustering(n_clusters = 2 , affinity = 'rbf' )
# Training the model and Storing the predicted cluster labels
labels_rbf = spectral_model_rbf.fit_predict(X_principal)# Building the label to colour mapping
colours = {}
colours[ 0 ] = 'b'
colours[ 1 ] = 'y'
# Building the colour vector for each data point
cvec = [colours[label] for label in labels_rbf]
# Plotting the clustered scatter plot
b = plt.scatter(X_principal[ 'P1' ], X_principal[ 'P2' ], color = 'b' );
y = plt.scatter(X_principal[ 'P1' ], X_principal[ 'P2' ], color = 'y' );
plt.figure(figsize = ( 9 , 9 ))
plt.scatter(X_principal[ 'P1' ], X_principal[ 'P2' ], c = cvec)
plt.legend((b, y), ( 'Label 0' , 'Label 1' ))
plt.show()
b) affinity=”nearest_neighbors”
# Building the clustering model
spectral_model_nn = SpectralClustering(n_clusters = 2 , affinity = 'nearest_neighbors' )
# Training the model and Storing the predicted cluster labels
labels_nn = spectral_model_nn.fit_predict(X_principal)
Step 5: Evaluate the results
# List of different values of affinity
affinity = [ 'rbf' , 'nearest-neighbours' ]
# List of Silhouette Scores
s_scores = []
# Evaluating the performance
s_scores.append(silhouette_score(X, labels_rbf))
s_scores.append(silhouette_score(X, labels_nn))
print (s_scores)
Step 6: Compare the performances
# Plotting a Bar Graph to compare the models
plt.bar(affinity, s_scores)
plt.xlabel( 'Affinity' )
plt.ylabel( 'Silhouette Score' )
plt.title( 'Comparison of different Clustering Models' )
plt.show()
First, your interview preparation enhances your data structure concepts with the Python DS course.